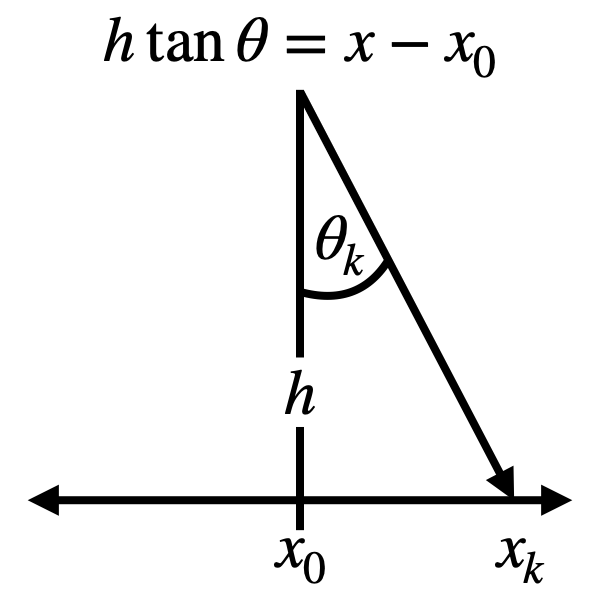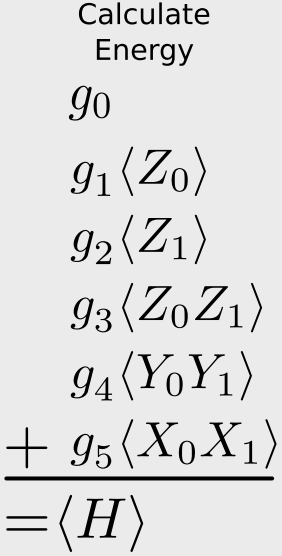Maximum Entropy Distributions

I think the method of maximum entropy to obtain probability distributions is so cool. You take a few knowns or constraints, and then maximize information entropy subject to these conditions and voila! you have a unique probability distribution. The cool thing is that these maximum entropy distributions are quite common, so this is a neat way of re-deriving many of the distibutions we encounter day-to-day. For me that alone is worth the cost of entry. But from an information-theoretic perspective, these will be the least biased prior distributions (we maximize our ignorance) so subsequent experiments a la Bayes’ theorem will maximize the information gained. Moreover, many physical patterns found in nature tend toward maximum entropy probability distributions. So even as a way to understand the world, maximum entropy is a very useful and deep tool.

Here are some common probability distributions and how to derive them from the principle of maximum entropy.

Table of Contents

1. Discrete uniform distribution
2. Continuous uniform distribution
3. Cauchy distribution
4. Exponential distribution
5. Gaussian distribution
6. Bernoulli distribution
7. Binomial distribution

Discrete uniform distribution

For the discrete case, consider \(N\) different possibilities, e.g. \(i \in X = \{1,2,\ldots,N\}\), and we have no other information other than the constraint that the probabilities \(p_i\) sum to 1. In this case, we maximize

subject to

by the method of Lagrange multipliers. So we take the derivative with respect to \(p_i\) of the Lagrangian

and we set the result equal to zero, as this is a maximization. Note that the second derivative is negative, indicating we are at a maximum, e.g.

and \(p_i\) is always positive. Therefore, we find that

and plugging into our normalization expression yields

which yields the discrete uniform probability distribution,

This is the maximum entropy distribution for the case with \(N\) possible outcomes with no other information given (other than our probabilities are normalized).

Continuous uniform distribution

This is similar, to the discrete case we just saw, but now assume that the random variable \(x\) can take any value in \([a,b]\). Then we want to maximize

subject to

which gives us our Lagrangian

differentiating the above with respect to \(p(x)\) and setting to zero gives

which gives us an expression for \(p(x)\) as

Like before, we can solve for \(\lambda_0\) by plugging the result back in our normalization expression to get

yielding

which is the continuous uniform distribution over \([a,b]\).

Cauchy distribution

The Cauchy distribution can be obtained in a similar way to the continuous uniform distribution, but in a particular geometric configuration. Consider the relationship between and angle \(\theta_k\) and a point \(x_k\) on a line some distance away, as illustrated in the diagram below. In this case we want to consider the case where our random variable \(\theta\) is an angle is on \([-\pi/2, \pi/2]\) and we don’t know anything else about the underlying distribution other than it is normalized. So we maximize

subject to

Now, from the previous section we know that the MaxEnt procedure would result in \(p(\theta) = 1/\pi\), which is obviously not the Cauchy distribution. To get the Cauchy distribution, we actually want to consider this case but in terms of a distribution over \(x\), where the relationship between \(x\) and \(\theta\) is given by \(h \tan \theta = x - x_0\), where \(h\) and \(x_0\) are arbitrary parameters.

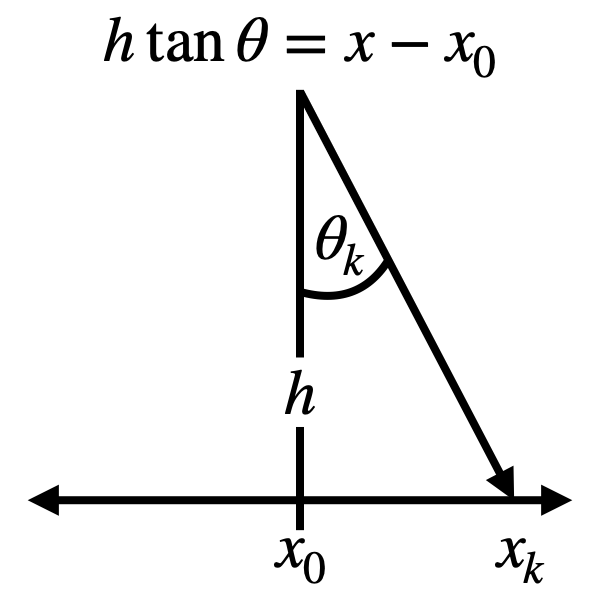
Relationship between \(\theta\) and \(x\). Here we want to consider the case where we don’t know anything about the underlying probability distribution of \(\theta\) other than that it is supported on \([-\pi/2, \pi/2]\) and that is is normalized, and we want this result as a distribution on \(x\). \(h\) and \(x_0\) are arbitrary parameters.

Since we have the relationship between \(\theta\) and \(x\), and the relationship is defined over \(\theta \in [-\pi/2,\pi/2]\), we can do a change of variables to get \(p(x)\) instead of \(p(\theta)\) and then carry out the maximization of entropy. To do the change of variables, we need

so that

For the limits on integration, we can easily see that

\(\tan (\pi/2) \to \infty\) and \(\tan (-\pi/2) \to -\infty\)

so \(x \in (-\infty,\infty)\). All together, we now want to maximize

subject to \(\int_{-\infty}^{\infty} p(x) dx = 1\) therefore, our Lagrangian is

and carrying out the maximization yields

which gives

substituting this into the normalization condition allows us to eliminate the \(\lambda_0\)

therefore, we get

So for sampling random angles and not knowing anything about the underlying distribution (e.g. \(\theta\) is continuous uniform), we see that the resulting distribution over \(x\) is a Cauchy distribution, when \(x\) and \(\theta\) have the relationship illustrated above.

Exponential distribution

Now extend the continuous distribution to the case where we have a known expected value of \(x = \mu\). We will limit ourselves to the support \([0,\infty)\). As before we maximize

but now subject to

which gives us our Lagrangian

differentiating the above with respect to \(p(x)\) and setting to zero gives

which gives us an expression for \(p(x)\) as

this results in the following expressions for our constraints:

where \(\frac{-1}{\lambda_1} < 0\) in order for the integral to converge. For the second constraint we have

Dividing the two constraints by each other allows us to solve for \(\lambda_1\):

and then from the normalization we get

which means \(\exp \left(\lambda_0 - 1\right) = 1/\mu\) and so from knowing a fixed mean, we obtain the exponential distribution over \([0,\infty)\)

Gaussian distribution

Now consider the case where we have a known mean \(\mu\) and variance \(\sigma^2\). We will consider \(x \in (-\infty,\infty)\). Because variance is the expectation of the squared deviation of a random variable \(x\) from its mean, it suffices to introduce the constraint

which we will consider along with normalization when maximizing the entropy. This leads to the Lagrangian

which, when differentiated with respect to \(p(x)\) and set equal to zero, yields

which gives us an expression for \(p(x)\) as

For the first constraint, we find that

And for the second constraint we find

Which allows us to say that

Putting this all together yields the Gaussian, or normal distribution

Bernoulli distribution

Moving back to the discrete case, let’s consider when a random variable \(k\) is either \(0\) or \(1\), i.e. \(k \in \{0,1\}\) and the expected value of \(k\) is \(\bar{p}\). This results in the Lagrangian

Maximizing this Lagrangian gives

which yields the probability mass function \(p_k\)

Taking care of the first constraint,

since \(k\) is either \(0\) or \(1\). Taking care of the second constraint,

again, since \(k\) is either \(0\) or \(1\). Then we can solve for \(\lambda_1\),

which means that

Putting this all together we have

Which is the Bernoulli distribution

for when \(0 \leq \bar{p} \leq 1\) and \(k\) is either \(0\) or \(1\).

Binomial distribution

This is the case where we compute the probability for having \(N\) successes in \(M\) trials. The constraint here is the expected number of successes \(\langle N \rangle\). Note that this will depend on the number of trials, and since we only care abut the number of successes, and not the order in which they were taken, we need to use the generalized form of entropy

where \(m(N)\) is the Lebesgue measure, which accounts for the fact that we need to account for the fact that we are indifferent to the number of ways \(N\) can be accomplished. This is essentially the prior probability we assign to the different outcomes. For example, in the uniform distribution we had no reason to favor one proposition \(p_i\) over another, thus the principle of indifference led us to assign \(m(i) = 1\) for all \(i\), and the result led to each outcome being equally likely. But this is not always the case in combinatoric problems, for example, since (without replacement) there are 4 ways to pick a unique object out of a set of 4 unique objects, but 6 ways to pick out 2 objects out of the same set. So we would not expect the probabilities for 2 objects to be on the same scale as picking out 1 object; our prior information leads us to favor 4 choose 2 over 4 choose 1 – there are more ways it could happen. The measure \(m(N)\) allows us to account for that.

In other words, for this combinatoric problem,

(As a chemist, I think of \(m(N)\) as event degeneracy.) Now, moving on, we are in addition to the normal entropy and normalization, constrained by the information \(\sum_N^M N p_N = \langle N \rangle = \mu\) Therefore, our Lagrangian reads

which leads to the maximization

so that

and we chose the combinatoric measure because for each possible number of successes \(N\), there are \(M!/N!(M-N)!\) different ways of achieving this given \(M\) trials.

Solving for the first constraint:

where we multiplied by \(1\) to the power of \(M-N\), which just equals one, in the first line in order to make use of the binomial formula and eliminate the sum. The inversion in the last line is made possible because the exponential is always greater than zero.

For the next constraint,

In fairness, I used WolframAlpha to finally eliminate the sum after the second line. If we let \(p \leftarrow \mu/M\), then we can finally see that

which we can obtain because \(p > 0\).

Okay. Putting it all together now:

and

which lets us finally show that

or, simply,

which is the binomial distribution.

Others

There are plenty others, like the Poisson, beta, and von Mises distributions which can be derived in a like manner. I may add more here if I get to it. Until then, check out the table from Wikipedia.

Variational Quantum Eigensolver (VQE) Example

Launch the interactive notebook:

Table of Contents

1. Introduction
2. Qubits, gates, and all that
3. Make that Hamiltonian!
4. A first attempt at a quantum circuit
5. A “real” quantum circuit
6. A “real” measurement of the energy
7. Appendix: All together now

Introduction

The variational quantum eigensolver (VQE) is a hybrid classical-quantum algorithm that variationally determines the ground state energy of a Hamiltonian.

It’s quantum in the sense that the expectation value of the energy is computed via a quantum algorithm, but it is classical in the sense that the energy is minimized with a classical optimization algorithm.

From a molecular electronic structure perspective, it is equivalent to computing the Full Configuration Interaction (FCI) for a given basis.

Quantum computing can be a little unintuitive, so it helps to see a working example. Although we won’t actually do any “real” quantum computing, the methods can be understood from a linear algebra perspective. So that’s what we are going to try and do for the VQE.

The problem we want to tackle is to implement the VQE to compute the energy of molecular hydrogen (H\(_2\)) in a minimal basis. We will base this implementation off the really neat paper

O’Malley, Peter JJ, et al. “Scalable quantum simulation of molecular energies.” Physical Review X 6.3 (2016): 031007.

In the O’Malley paper, they implement the VQE on a real quantum computer to compute the potential energy surface of H\(_2\). The schematic we are going to follow can be seen below, and we are going to implement the “software”.

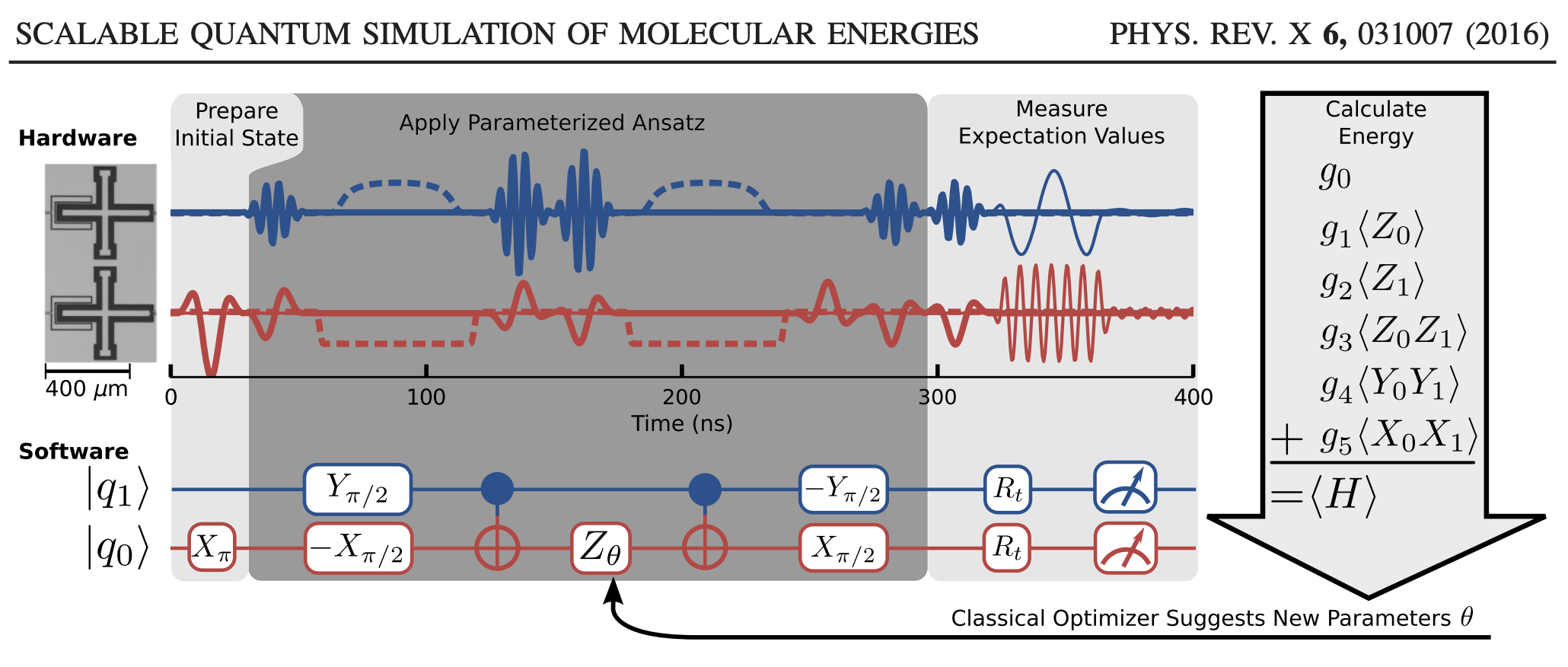
Here’s the big, overarching plan:

1. Put the Hamiltonian in the computational (qubit) basis.
2. Obtain a variational ansatz to parameterize the wave function.
3. Represent this ansatz as a quantum circuit.
4. Given this circuit, measure the expectation value of Hamiltonian (energy).
5. Vary the circuit parameters until the energy is minimized.

We’ll look at these in turn, but first, let’s look at single qubit states and some common matrices used to operate on them. This will set the groundwork for building up our VQE procedure.

Qubits, gates, and all that

First, let’s define some of the common quantum operators, gates, and states we want to work with. For starters, here are the identity and Pauli spin matrices:

Two other important gates are the Hadamard matrix and phase matrix:

Since for a single qubit the two basis states are \(|\psi\rangle = \begin{pmatrix} |0\rangle\\ |1\rangle \end{pmatrix}, \quad \mathrm{meaning} \qquad |0\rangle = \begin{pmatrix} 1\\ 0 \end{pmatrix}\quad |1\rangle = \begin{pmatrix} 0\\ 1 \end{pmatrix}\)

we can define projection matrices, which are useful for defining, among other things, controlled gates (like CNOT, which we will see in a bit).

Also useful for single qubits, are the rotation matrices:

So putting all these together for future use, we have:

import numpy as np
np.set_printoptions(precision=4,suppress=True)


# Pauli matrices
I  = np.array([[ 1, 0],
               [ 0, 1]])
Sx = np.array([[ 0, 1],
               [ 1, 0]])
Sy = np.array([[ 0,-1j],
               [1j, 0]])
Sz = np.array([[ 1, 0],
               [ 0,-1]])

# Hadamard matrix
H = (1/np.sqrt(2))*np.array([[ 1, 1],
                             [ 1,-1]])

# Phase matrix
S = np.array([[ 1, 0],
              [ 0,1j]])

# single qubit basis states |0> and |1>
q0 = np.array([[1],
               [0]])
q1 = np.array([[0],
               [1]])

# Projection matrices |0><0| and |1><1|
P0  = np.dot(q0,q0.conj().T)
P1  = np.dot(q1,q1.conj().T)


# Rotation matrices as a function of theta, e.g. Rx(theta), etc.
Rx = lambda theta : np.array([[    np.cos(theta/2),-1j*np.sin(theta/2)],
                              [-1j*np.sin(theta/2),    np.cos(theta/2)]])
Ry = lambda theta : np.array([[    np.cos(theta/2),   -np.sin(theta/2)],
                              [    np.sin(theta/2),    np.cos(theta/2)]])
Rz = lambda theta : np.array([[np.exp(-1j*theta/2),                0.0],
                              [                0.0, np.exp(1j*theta/2)]])

Next, using these single qubit operations, we can build up some common two-qubit states and operations. By and large, moving from single to multiple qubits just involves tensor products of single qubit states and gates. Note that we number our qubits from bottom to top in this example, so qubit-1 is on top and qubit-0 is on bottom; e.g. in the figure:

So for our two qubits the basis looks like

so that, e.g.

For two qubits, useful are the CNOT\(_{01}\) and CNOT\(_{10}\), where the first digit is the “control” qubit and the second is the “target” qubit. (Again, recall that in the O’Malley paper, we define qubit-1 as the “top” qubit, and qubit-0 as the “bottom” qubit, so if you change the qubit numbering the definitions will be swapped).

They can be defined as the sum of two tensor products:

The SWAP gate does what you’d expect, swapping qubit 1 and qubit 0:

Most other operations are just simple tensor products of the single qubit operations. Like if you want to apply a Pauli X gate to qubit 1 and a Pauli Y gate to qubit 0, it’s just \(X_1 \otimes Y_0\):

Okay, let’s get some of these coded up for later, and if we need any products, we know we can just np.kron them later as needed

from scipy.linalg import block_diag

# CNOTij, where i is control qubit and j is target qubit
CNOT10 = np.kron(P0,I) + np.kron(P1,Sx) # control -> q1, target -> q0
CNOT01 = np.kron(I,P0) + np.kron(Sx,P1) # control -> q0, target -> q1

SWAP   = block_diag(1,Sx,1)

Make that Hamiltonian!

Now we have our building blocks, we need to think about how to represent the Hamiltonian, which is usually in the fermion basis, in the basis of qubits. There are a few ways to do this, but the most common are the Jordan-Wigner (JW) transformation and the Bravyi-Kitaev (BK) transformation.

According to the O’Malley paper, using the BK-transformed Hamiltonian and exploiting some of the symmetry in the H\(_2\) molecule, the Hamiltonian can be represented by only two qubits. (Nice.) The Hamiltonian has five components:

It general, the coefficients \(g_i\) can be obtained from a cheap Hartree-Fock calculation.

So let’s build a Hamiltonian for the H\(_2\) molecule with a bond length of 0.75 A. We will also also add the nuclear repulsion energy nuclear_repulsion. The parameters we use can be found in Table 1 of the Appendix in the O’Malley paper, though for the nuclear repulsion energy you have to calculate yourself (I used Gaussian).

# See DOI: 10.1103/PhysRevX.6.031007
# Here, we use parameters given for H2 at R=0.75A
g0 = -0.4804
g1 = +0.3435
g2 = -0.4347
g3 = +0.5716
g4 = +0.0910
g5 = +0.0910

nuclear_repulsion = 0.7055696146

With all this, we can build the Hamiltonian, Hmol, explicitly in matrix form by taking tensor products, also known as Kronecker products (using np.kron), of the single-qubit matrix operators we built previously.

Hmol = (g0 * np.kron( I, I) + # g0 * I
        g1 * np.kron( I,Sz) + # g1 * Z0
        g2 * np.kron(Sz, I) + # g2 * Z1
        g3 * np.kron(Sz,Sz) + # g3 * Z0Z1
        g4 * np.kron(Sy,Sy) + # g4 * Y0Y1
        g5 * np.kron(Sx,Sx))  # g5 * X0X1

And let’s take a look at the Hamiltonian matrix:

print(Hmol)

    [[ 0.0000+0.j  0.0000+0.j  0.0000+0.j  0.0000+0.j]
     [ 0.0000+0.j -1.8302+0.j  0.1820+0.j  0.0000+0.j]
     [ 0.0000+0.j  0.1820+0.j -0.2738+0.j  0.0000+0.j]
     [ 0.0000+0.j  0.0000+0.j  0.0000+0.j  0.1824+0.j]]

Since we have the Hamiltonian in the computational basis, let’s just diagonalize it to get the energy (lowest eigenvalue). By adding the nuclear repulsion energy to the result we should get the same result as a Full Configuration Interaction (FCI) calculation.

electronic_energy = np.linalg.eigvalsh(Hmol)[0] # take the lowest value
print("Classical diagonalization: {:+2.8} Eh".format(electronic_energy + nuclear_repulsion))
print("Exact (from G16):          {:+2.8} Eh".format(-1.1457416808))

    Classical diagonalization: -1.1456295 Eh
    Exact (from G16):          -1.1457417 Eh

Considering that the Hamiltonian elements had a precision of 1E-04, this is very good agreement. However, this approach utilizes a classical algorithm to obtain the eigenvalues. We want to see if we can obtain the eigenvalues using a quantum circuit.

A first attempt at a quantum circuit

The usual input for quantum algorithms is to start in the \(\vert00\cdots\rangle\) state. This is represented by a zero vector, with the first element set to 1. Because our Hamiltonian for H\(_2\) only requires two qubits, we will start with the state \(\vert01\rangle\). To obtain this from \(\vert00\rangle\), we just need to act on the zeroth qubit with the Pauli X operator. This is the first step in the quantum circuit in the figure I showed above from the O’Malley paper. (They apply X\(_{\pi}\); same thing.)

# initial basis, put in |01> state with Sx operator on q0
psi0 = np.zeros((4,1))
psi0[0] = 1
psi0 = np.dot(np.kron(I,Sx),psi0)
print(psi0)

[[ 0.]
 [ 1.]
 [ 0.]
 [ 0.]]

We haven’t defined our VQE ansatz yet, but before we do, let’s write a function to return the expected value of the Hamiltonian Hmol given an ansatz, its parameter theta, and the initial state psi0. This ansatz will eventually be encoded by the quantum circuit.

def expected(theta,ansatz,Hmol,psi0):
    circuit = ansatz(theta[0])
    psi = np.dot(circuit,psi0)
    return np.real(np.dot(psi.conj().T,np.dot(Hmol,psi)))[0,0]

With the expectation value in hand, we now define an ansatz. In the O’Malley paper, they utilize the Unitary Coupled Cluster (UCC) ansatz, which in this case depends only on a single parameter \(\theta\):

so that a parameterized wave function \(\vert\psi(\theta)\rangle\) for the ground state of H\(_2\) is given as

and \(X_0Y_1\) is the tensor product of the Pauli-X on qubit 0 and Pauli-Y on qubit 1.

Before thinking about how we might represent \(U(\theta)\) as a series of quantum gates, let’s plug it into the expression

(Note that as long as \(\psi\) is normalized and \(U\) is unitary, we can ignore the normalization \(\langle \psi \vert U^{\dagger}(\theta)U(\theta)\vert\psi\rangle\), since it always equals 1.)

Given the ansatz and the initial state psi0, we can minimize expected() using the classical optimizers in the scipy package. So straightforwardly plugging in and minimizing yields the lazy result:

from scipy.linalg import expm
from scipy.optimize import minimize

# our UCC ansatz, not yet represented in terms of quantum gates
ansatz = lambda theta: expm(-1j*np.array([theta])*np.kron(Sy,Sx))

# initial guess for theta
theta  = [0.0]
result = minimize(expected,theta,args=(ansatz,Hmol,psi0))
theta  = result.x[0]
val    = result.fun

print("Lazy VQE: ")
print("  [+] theta:  {:+2.8} deg".format(theta))
print("  [+] energy: {:+2.8} Eh".format(val + nuclear_repulsion))

Lazy VQE: 
  [+] theta:  -0.11487186 deg
  [+] energy: -1.1456295 Eh

Which equals the result we got from diagonalization of the Hamiltonian. So we know that the UCC ansatz works! But we were lazy and didn’t bother to think about how the quantum computer would compute the exponential. So, how do we represent the UCC ansatz in terms of quantum gates acting on the initial qubit state?

A “real” quantum circuit

So before we saw the UCC ansatz works, but we cheated by keeping it as a matrix exponential. This is not a suitable form for a quantum computer. Let’s do better.

According to the O’Malley paper , we can represent \(U(\theta)\) for this problem as:

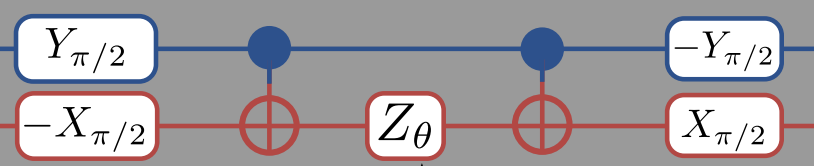
This means that we should change our ansatz to read

# read right-to-left (bottom-to-top?)

ansatz = lambda theta: (np.dot(np.dot(np.kron(-Ry(np.pi/2),Rx(np.pi/2)),
                        np.dot(CNOT10, 
                        np.dot(np.kron(I,Rz(theta)),
                               CNOT10))),
                               np.kron(Ry(np.pi/2),-Rx(np.pi/2))))

Note that while you read the the circuit diagram left-to-right, when you read the matrix expression above it is better read right-to-left. The right-most matrices are applied to the state first, so that the first gates we apply are -R\(_x(\pi/2)\) to qubit-0 and R\(_y(\pi/2)\) to qubit-1. Also note that when we apply these two gates, it is simultaneous so the “total” gate is really -R\(_y(\pi/2) \otimes\)R\(_x(\pi/2)\).

theta  = [0.0]
result = minimize(expected,theta,args=(ansatz,Hmol,psi0))
theta  = result.x[0]
val    = result.fun

print("VQE: ")
print("  [+] theta:  {:+2.8} deg".format(theta))
print("  [+] energy: {:+2.8} Eh".format(val + nuclear_repulsion))

VQE: 
  [+] theta:  +2.9118489 deg
  [+] energy: -1.1456295 Eh

Which is the correct answer! Since we can now compute the expectation value of our Hamiltonian using quantum gates, we can pass the computed energy to a classical optimizer, which gives new parameters for the quantum gates. When this process is repeated until convergence, we obtain the FCI ground state energy. Also, once we have the optimized wave function parameters, the ground state can be easily reconstructed for additional simulations, etc.

You might have noticed, though, that the above is still not sufficient for a quantum computer. The reason is that although we have represented our wave function with quantum gates, the measurement of the expectation value is still poorly defined as a physical operation. Even if you have prepared your qubits to represent a molecular wave function, measuring the expectation value of the Hamiltonian is not simply accomplished physically by applying a “Hamiltonian operation”.

An analogy: similar to classical computation, you might want a string, or float, or whatever as the “true” output of your function, but for the computer to compute it for you – it needs to ultimately be in binary. Same thing for the quantum computer. Our function should ultimately return the energy, but it needs to process this in terms of quantum bits.

A “real” measurement of the energy

All that is to say that we were cheating again. Experimentally, the “only” measurements we can make are those which probe the final quantum state of the qubits. What we need a way to connect measurements of qubits to an expression for the expectation value of the molecular electronic Hamiltonian.

Put another way, the problem stems back to our definition of the expected value:

def expected(theta,ansatz,Hmol,psi0):
    circuit = ansatz(theta[0])
    psi = np.dot(circuit,psi0)
    return np.real(np.dot(psi.conj().T,np.dot(Hmol,psi)))[0,0]

Simply dotting in Hmol with the wave function will not work, because physically we don’t have a measuring apparatus for “energy”. We can, however, measure the state of each qubit by measuring the spin (\(\hat{\mathrm{S}}_z\)) of each qubit. We need to reduce the Hamiltonian’s expected value into these types of “easy” projective measurements that can be done in the computational basis. These are sums of Pauli measurements.

Now in some respects, we are already halfway there. For a normalized wave function \(\vert\psi'\rangle\):

and using the definition of our H\(_2\) Hamiltonian in the computational basis we have:

meaning that, given our wave function in the computational basis, if we can compute the expected value of the (products of) Pauli operators, we can relate this to the expected value of the Hamiltonian through the sum given above. This is given in that figure:

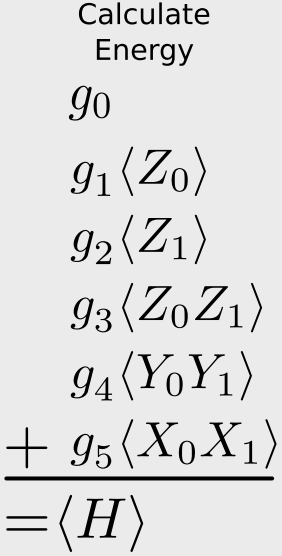
Let’s go a step further, though. It would be even better if we could relate the above expression to a single type of Pauli measurement, that is, measuring the spin of just one qubit. Then we don’t need to have multiple measurement apparatus.

Thankfully, there is a way to do this. The trick is to apply an additional unitary transformation at the end of the circuit so that, by measuring the spin of the top qubit, we can obtain any Pauli measurement. In our case, that means relating each of the the \(\langle \hat{O}_i\rangle\) quantities to the expected value of \(\langle Z_1 \otimes \mathbf{I}\rangle\) by some appropriate unitary operator. This is what is meant by the R\(_t\) gates in this part of the figure. The R\(_t\) are the unitaries we are talking about.

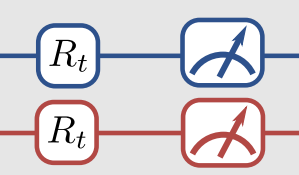
The little measuring gauge means we finally apply the measurement. Because we apply a particular form of the unitaries, we only need to measure the state of qubit-1 like we talked about above, but that’s not necessarily the only way to go about it.

You can find a table of some of these transformations here, but here are a few examples:

For example, the simplest case is if you want to measure \(Z_1 \otimes \mathbf{I}\). Then you don’t have to do anything:

But if you want to measure \(Y_1 \otimes \mathbf{I}\), then

For \(\mathbf{I} \otimes Z_0\), we have to apply the SWAP gate

And as a final example, for \(X_1Z_0\), (caveat: we have different qubit ordering compared to the Microsoft documentation, so our CNOT\(_{10}\) vs CNOT\(_{01}\) definitions are swapped)

Since you can think of these unitary transformations either acting on the operator, or acting on the state, the end result is that by applying the particular transformation and then measuring \(Z_1\) you can get any Pauli measurement you want.

It might be easier to see by example. Let’s see how this plays out for our Hamiltonian.

We will update the function expected() to projective_expected(), and remove the Hmol argument. In our case, this function will include the hard-coded representation of the Hamiltonian, in terms of measuring \(Z_1\).

def projective_expected(theta,ansatz,psi0):
    # this will depend on the hard-coded Hamiltonian + coefficients
    circuit = ansatz(theta[0])
    psi = np.dot(circuit,psi0)
    
    # for 2 qubits, assume we can only take Pauli Sz measurements (Sz \otimes I)
    # we just apply the right unitary for the desired Pauli measurement
    measureZ = lambda U: np.dot(np.conj(U).T,np.dot(np.kron(Sz,I),U))
    
    energy = 0.0
    
    # although the paper indexes the Hamiltonian left-to-right (0-to-1) 
    # qubit-1 is always the top qubit for us, so the tensor pdt changes
    # e.g. compare with the "exact Hamiltonian" we explicitly diagonalized
    
    # <I1 I0>
    energy += g0 # it is a constant

    # <I1 Sz0>
    U = SWAP
    energy += g1*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sz1 I0>
    U = np.kron(I,I)
    energy += g2*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sz1 Sz0>
    U = CNOT01
    energy += g3*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sx1 Sx0>
    U = np.dot(CNOT01,np.kron(H,H))
    energy += g4*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sy1 Sy0>
    U = np.dot(CNOT01,np.kron(np.dot(H,S.conj().T),np.dot(H,S.conj().T)))
    energy += g5*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    return np.real(energy)[0,0]

With the expectation value now defined in terms of measuring the spin of the zero-th qubit, let’s carry out the VQE procedure:

theta  = [0.0]
result = minimize(projective_expected,theta,args=(ansatz,psi0))
theta  = result.x[0]
val    = result.fun

print("VQE: ")
print("  [+] theta:  {:+2.8} deg".format(theta))
print("  [+] energy: {:+2.8} Eh".format(val + nuclear_repulsion))

VQE: 
  [+] theta:  +2.9118489 deg
  [+] energy: -1.1456295 Eh

Success! We get the same energy (and theta) as the previous VQE circuit, but now all measurements are related back to the result of measuring the spin of the qubit.

Appendix: All together now

Here’s all of the pieces together in one place

import numpy as np
from scipy.linalg import block_diag
from scipy.optimize import minimize

np.set_printoptions(precision=4,suppress=True)


# Pauli matrices
I  = np.array([[ 1, 0],
               [ 0, 1]])
Sx = np.array([[ 0, 1],
               [ 1, 0]])
Sy = np.array([[ 0,-1j],
               [1j, 0]])
Sz = np.array([[ 1, 0],
               [ 0,-1]])

# Hadamard matrix
H = (1/np.sqrt(2))*np.array([[ 1, 1],
                             [ 1,-1]])

# Phase matrix
S = np.array([[ 1, 0],
              [ 0,1j]])

# single qubit basis states |0> and |1>
q0 = np.array([[1],
               [0]])
q1 = np.array([[0],
               [1]])

# Projection matrices |0><0| and |1><1|
P0  = np.dot(q0,q0.conj().T)
P1  = np.dot(q1,q1.conj().T)


# Rotation matrices as a function of theta, e.g. Rx(theta), etc.
Rx = lambda theta : np.array([[    np.cos(theta/2),-1j*np.sin(theta/2)],
                              [-1j*np.sin(theta/2),    np.cos(theta/2)]])
Ry = lambda theta : np.array([[    np.cos(theta/2),   -np.sin(theta/2)],
                              [    np.sin(theta/2),    np.cos(theta/2)]])
Rz = lambda theta : np.array([[np.exp(-1j*theta/2),                0.0],
                              [                0.0, np.exp(1j*theta/2)]])

# CNOTij, where i is control qubit and j is target qubit
CNOT10 = np.kron(P0,I) + np.kron(P1,Sx) # control -> q1, target -> q0
CNOT01 = np.kron(I,P0) + np.kron(Sx,P1) # control -> q0, target -> q1

SWAP   = block_diag(1,Sx,1)

# See DOI: 10.1103/PhysRevX.6.031007
# Here, we use parameters given for H2 at R=0.75A
g0 = -0.4804
g1 = +0.3435
g2 = -0.4347
g3 = +0.5716
g4 = +0.0910
g5 = +0.0910

nuclear_repulsion = 0.7055696146

Hmol = (g0 * np.kron( I, I) + # g0 * I
        g1 * np.kron( I,Sz) + # g1 * Z0
        g2 * np.kron(Sz, I) + # g2 * Z1
        g3 * np.kron(Sz,Sz) + # g3 * Z0Z1
        g4 * np.kron(Sy,Sy) + # g4 * Y0Y1
        g5 * np.kron(Sx,Sx))  # g5 * X0X1

electronic_energy = np.linalg.eigvalsh(Hmol)[0] # take the lowest value
print("Classical diagonalization: {:+2.8} Eh".format(electronic_energy + nuclear_repulsion))
print("Exact (from G16):          {:+2.8} Eh".format(-1.1457416808))

# initial basis, put in |01> state with Sx operator on q0
psi0 = np.zeros((4,1))
psi0[0] = 1
psi0 = np.dot(np.kron(I,Sx),psi0)


# read right-to-left (bottom-to-top?)
ansatz = lambda theta: (np.dot(np.dot(np.kron(-Ry(np.pi/2),Rx(np.pi/2)),
                        np.dot(CNOT10, 
                        np.dot(np.kron(I,Rz(theta)),
                               CNOT10))),
                               np.kron(Ry(np.pi/2),-Rx(np.pi/2))))

def projective_expected(theta,ansatz,psi0):
    # this will depend on the hard-coded Hamiltonian + coefficients
    circuit = ansatz(theta[0])
    psi = np.dot(circuit,psi0)
    
    # for 2 qubits, assume we can only take Pauli Sz measurements (Sz \otimes I)
    # we just apply the right unitary for the desired Pauli measurement
    measureZ = lambda U: np.dot(np.conj(U).T,np.dot(np.kron(Sz,I),U))
    
    energy = 0.0
    
    # although the paper indexes the hamiltonian left-to-right (0-to-1) 
    # qubit-1 is always the top qubit for us, so the tensor pdt changes
    # e.g. compare with the "exact Hamiltonian" we explicitly diagonalized
    
    # <I1 I0> 
    energy += g0 # it is a constant

    # <I1 Sz0>
    U = SWAP
    energy += g1*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sz1 I0>
    U = np.kron(I,I)
    energy += g2*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sz1 Sz0>
    U = CNOT01
    energy += g3*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sx1 Sx0>
    U = np.dot(CNOT01,np.kron(H,H))
    energy += g4*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    # <Sy1 Sy0>
    U = np.dot(CNOT01,np.kron(np.dot(H,S.conj().T),np.dot(H,S.conj().T)))
    energy += g5*np.dot(psi.conj().T,np.dot(measureZ(U),psi))

    return np.real(energy)[0,0]

theta  = [0.0]
result = minimize(projective_expected,theta,args=(ansatz,psi0))
theta  = result.x[0]
val    = result.fun

# check it works...
#assert np.allclose(val + nuclear_repulsion,-1.1456295)

print("VQE: ")
print("  [+] theta:  {:+2.8} deg".format(theta))
print("  [+] energy: {:+2.8} Eh".format(val + nuclear_repulsion))

Classical diagonalization: -1.1456295 Eh
Exact (from G16):          -1.1457417 Eh
VQE: 
  [+] theta:  +2.9118489 deg
  [+] energy: -1.1456295 Eh

(Some) COVID-19 deaths are probably vastly underreported pending

Update 07/18/2020: “Unclassified” includes “pending”

The mystery of the excess “unclassified” deaths has been resolved, thanks to here and here.

Long story short, the deaths in R00-R99 include “pending” cause of death. So the changes in the R00-R99 deaths are not due to fraudulent data, but rather a very, very slow reporting process. States are required to report timely deaths, but because analyzing the cause of death can take months (yes, months) those cases that are pending are put in the “unclassified” category. This includes potentially sensitive and complicated deaths like drug overdose. Over time these extra unclassified deaths get resolved.

Here is a chart from the CDC (Figure 3), which shows how the percent of “unclassified deaths” at a certain time decreases over a typical (read: non-COVID-19) year as the deaths get re-classified and put into appropriate categories.

For the sake of intellectual honesty, I’m leaving the post unedited to record my thought process. But I’m glad it appears that the “unclassified deaths” are not due to fraudulent COVID-19 reporting. (Though the pace of death classification can be strikingly slow!)

The CDC gives the number of deaths reported and coded for a given week, giving insight into how many people died of what cause.

The data is not perfect: It only counts deaths received in that period, so it might not represent the deaths that actually occurred in that period. And some deaths may be provisional or incomplete due to lag between time of death and completion of death certificate. This is especially true in the most recent weeks, which are often incomplete (especially due to COVID-19) because of lag in counting. Regardless, it is helpful to see historical trends.

One category is especially interesting to explore and that is the “mysterious” deaths due to “Symptoms, signs and abnormal clinical and laboratory findings, not elsewhere classified (R00-R99)”. We will just refer to these as “Unclassified”.

Basically it is the junk drawer of deaths, but remains fairly constant from year to year.

Here’s a plot of Unclassified deaths in 2020 in the USA, compared with the previous 5 years as a baseline. I’ve also plotted COVID-19 deaths, where COVID-19 has been marked as the underlying cause.

You can see the dark blue line continuing to increase, even as the total COVID-19 deaths fall. The unclassified deaths are increasing several times the baseline.

Of course, the USA is big, so it helps to compare with some individual states. Here’s New York, New Jersey, and Massachusetts:

These Northeast states saw/reported huge COVID-19 deaths in April. The unclassified deaths are increasing for all, but a small proportion relative to those coded as due to COVID-19. But the unclassified deaths remain several standard deviations away from the baseline. It’s hard to see above, but the baseline is shaded light blue by plus-or-minus one standard deviation from the mean. (It’s easier to see below.)

Compare that to some of the southern states that saw a huge resurgence in COVID-19 cases in May and June, like Florida, Arizona, and Texas:

These states have reported far fewer deaths in total than the Northeastern states. But look at the relative numbers. In Florida and Texas, the unclassified deaths have now outpaced the COVID-19 deaths. In Arizona, unclassified and COVID-19 deaths are neck-and-neck. These states have an equal-to or larger proportion of unclassified deaths compared to COVID-19. In all cases (just like in the Northeast) the unclassified deaths are several (> 5) standard deviations (the light blue shading) away from the 5-year baseline. These death rates never fell; at best they plateaued.

No reporting is perfect and in every state we see the “mysterious” unclassified deaths increasing several times beyond the baseline — we are talking several standard deviations beyond the mean. This is not normal. And for some states, these deaths are more than, or nearly equal to, the number of deaths due to COVID-19.

Every state wants to re-open now that lockdown has drop-kicked the economy. I want to go back to normal (whatever that means) more than anything. But re-opening based on “lower death rates” is more complicated than it seems if the data is indeed this complicated.

I’m not saying that all these unclassified deaths are COVID-19. But it would be very strange if most of them were not. The worst interpretation is that these data are being fudged to justify re-opening. Best case would be a strained medical reporting system. Maybe there is another explanation that I can’t think of – after all, it’s been a strange year.

What does Trump talk about when he talks about COVID-19?

The code and details can be found on GitHub here.

Table of Contents

• Background
• Findings
  • What does Trump talk about?
  • Keywords for each day’s briefing
  • How positive/negative is Trump during his speeches?
  • What might be influencing Trump’s attitude?
• Details on Data Acquisition

Background

Since March 14, 2020, President Trump has given semi-regular press updates on the global COVID-19 outbreak. While this pandemic is impacting nearly every aspect of everyday life, it is important to understand how our leaders perceive and communicate the next steps as we tackle these unprecedented issues.

The New York Times (NYT) recently ran a fascinating article that painstakingly analyzed over 260,000 words Trump has publicly spoken about the novel coronavirus. It took three journalists at the NYT to review all these statements by hand, and they found that the President’s comments were particularly self-congratulatory, exaggerated, and startlingly lacking in empathy when compared to how often he praises himself and his administration.

I wondered, though, if a more data-driven approach to Trump’s remarks would yield any new insights. In particular, using data and natural language processing (NLP) to understand:

• What topics Trump thinks are particularly important?

• What are some of the keywords for each day’s briefing?

• Trump’s attitude (sentiment) during his speeches?

• What underlying factors in the news or world correlate with his message?

Given that all his remarks are publicly recorded on the White House webpage, I knew we had what we needed to answer these questions.

Findings

What does Trump talk about?

I wanted to get an idea of what topics Trump talks about during his briefings. To answer this, I used non-negative matrix factorization (NMF) to cluster keywords around certain topics. The number of topics and the interpretation of the topic is up to the scientist. There’s no right answer as this is an unsupervised learning problem, but I found that the topics made the most sense if you limit them to six.

The most important keywords are listed and my intepretation of the topic. For example, the first topic is clearly talking about new treatments, cures, and vaccines for COVID-19. We should expect this to be a topic duing his briefings! Other ones make sense to me as well, like economic recovery. I was a little surprised (OK maybe not too surprised) how often he remarked on his media coverage. And the COVID-19 Task Force topic generally seems to bring up how well his administration is handling the pandemic. This is consistent with what the NYT article found.

You can see for yourself below!

In general, when Trump speaks his statements fall into one of these topics 18% of the time. That’s pretty good coverage for our topics given that we limit ourselves to only 6 topics. That said, relatively speaking, what does he talk most about?

When Trump’s statements fall into one of these six topics, Trump talks about farmers, trade, and tariffs nearly 25% of the time (4.3% overall). If we lump this group in with the economic recovery topic, it seems Trump talks about the economy well over a third of the time, nearly double that of the actual health impact (vaccines and treatment). Another quarter of the time is spent commenting on the media and how his administration is handling the crisis. These are rough numbers, but the pattern emerges that Trump’s preferred topics are the economy and his image (combining both press coverage and his administration’s COVID Task Force).

Keywords for each day’s briefing

It’s interesting to see what Trump thinks is important each day. One way to address this is to pull out the top keywords for each day’s briefing. The technique we use is term-frequency inverse-document-frequency (TF-IDF) and treat each day’s briefing as a “document”. It’s a cheap and effective way to pull out those unique keywords that distinguish each day’s briefing.

Here’s an example of the important keywords found on March 14:

So here you can see that “mic” (or “microphone”) was a keyword of interest. Interestingly, Trump went on a bit of a rant during his talk because he was accused of touching the microphone:

Somebody said yesterday I touched the microphone. I was touching it because we have different height people and I’m trying to make it easy for them because they’re going to have to touch, because they wouldn’t be able to reach the mic; they wouldn’t be able to speak in the mic. So I’ll move the mic down. And they said, “Oh, he touched the microphone.” Well, if I don’t touch it, they’re going to have to touch it. Somebody is going to have to, so I might as well be the one to do it.

Amusing that the model identified this (somewhat) bizarre tangent.

You can see for yourself below. Near the beginning of the briefings, things seem much more focused on health-care and government action (“proactive”, “self swab”, “buyback”). But as the economy progressively gets worse (see March 23!) then we see more of an economic focus (“exchange”, “cure is worse than the problem”). The economic shutdown is no small deal!

You can also see the importance of oil in April. It wasn’t a huge issue early on, but you see it become more important starting around April 3, peaking around April 9. That day, if you recall, was when OPEC made huge cuts in oil production. So naturally it was a topic in Trump’s briefing that day!

How positive/negative is Trump during his speeches?

We can investigate how positive or negative Trump is speaking during his briefings. To do this, we look at the compound sentiment for each briefing using the Valence Aware Dictionary and sEntiment Reasoner (VADER). Although it was trained on social media, it works well for our purposes. It ranges from -1 (negative) to +1 (positive).

So given the statement: “I hate you!”, VADER assigns it a -1. But given the statement “I love you!” VADER assigns it a +1. For statements like “I love pizza, but hate the color red”, VADER gives it a compound sentiment of zero. For Trump, we take the average compound sentiment for a given day.

You can see that, on the whole, Trump is pretty positive-to-neutral. Politically, I think this would be better to lean positive during the briefings. Of course, you don’t want to be too positive either during these tough times!

On average, his sentiment lies around 0.4, with a standard deviation of 0.1. So leaning positive, but by no means elated, which is probably the right tone to hit.

It’s interesting to note the spike in Trump’s positivity on April 24. Was he really more positive than usual? The model suggests so — and he was!

POLITICO noticed then same thing, and ran an article about it. After getting rebuked the day before for claiming sunlight and ingesting Lysol as a cure for COVID-19, Trump took a more conventional approach. In this particular briefing, he didn’t bash any political opponents, didn’t talk about any unproven cures, or argue with reporters. He only predicted quick economic turnaround. The article states:

For a ritual that in recent days has displayed some the trappings of a political rally, the most unusual thing about the briefing was how conventional it was … There was no touting of unproven remedies, no swipes at political foes; only prediction of a swift economic rebound, praise for governors who are rolling out plans to reopen their states and updates on his administration’s public health and economic response to the crisis that has killed more than 50,000 Americans. (POLITICO 04/24/2020)

Fascinating to see the change in attitude reflected in the VADER analysis!

What might be influencing Trump’s attitude?

Perhaps more interesting is to try and find patterns in Trump’s sentiment. Initially, I noticed the big spike in sentiment on March 24, as well as a pretty big drop in sentiment on April 1. On March 24, there was a big stock market rally, and on April 1, the market suffered a few days of losses. I wondered: could it be that Trump’s mood is correlated with stock market performance?

To investigate, I plotted Trump’s sentiment versus the percent change in the closing value of the Dow Jones Industrial Average. On first look, you can see that the briefing sentiment shows some correlation with changes in the DJIA. If the market is doing bad, Trump is generally more negative, and if the market is doing well, Trump is more positive. It’s tough to say which direction the correlation goes (correlation is not causation!) but given that Trump usually holds his briefings later in the day, I’m inclined to think the market bears more influence on his mood. But the issues are complicated and there are many more variables at play, so take it with a grain of salt.

We can actually make the correlation between stock market and Trump’s mood a bit tighter. Below we have a regression plot, and find that the Pearson correlation is around +0.45. Note that we don’t include the cases where Trump gives a briefing on a weekend or holiday! (Which shouldn’t be correlated with the markets.) We also see that the R² is 0.2 with a p-value of 0.03. So the Dow daily variation can account for 20% of Trump’s sentiment and is statistically significant (p-value < 0.05). This is good enough to say that there is likely a moderate positive correlation between Trump’s sentiment and the market performance. Makes sense, as he prides himself on his business acumen and being able to keep the American economy strong. (No comment if that corresponds to reality.)

Details on Data Acquisition

The raw data was scraped from https://www.whitehouse.gov/remarks/ using requests and BeautifulSoup4. For now, all we explore Trump’s statements during the Coronavirus Task Force press meetings (which as of today, May 6, may be ending).

The president’s name is listed before he speaks, so once the page is downloaded locally, it is relatively easy to extract just Trump’s statements. We treat a “statement” as any of Trump’s spoken words separated by a newline. This gave a variety of statements, usually around 3 to 5 sentences long. If any statement was less than 16 words, we ignored it (these usually are statements like “Thank you John, next question”, etc.) as these are not meaningful. If a statement was too long (longer than 140 words) we split them into smaller chunks. This foresight allows us to use the BERT transformer in future work, which in the default model cannot handle sentences with more than 512 word embeddings.

Once the raw text was extracted to a pandas DataFrame, we applied standard text-cleaning routines to make all lowercase, remove stopwords, and add bigrams and trigrams (so mayor, de, blasio is not three separate words, but instead is treated as mayor_de_blasio, which is much more informative!).

Neural Networks by Analogy with Linear Regression

Most scientists are aware of the importance and significance of neural networks. Yet for many, neural networks remain mysterious and enigmatic.

Here, I want to show that neural networks are simply generalizations of something we scientists are perhaps more comfortable with: linear regression.

Regression models are models that find relationships among data. Linear regression models fit linear functions to data, like the \(y = mx + b\) equations we learned in algebra. If you have one variable, it’s single-variate linear regression; if you have more than one variable, it’s multi-variate linear regression.

One example of a linear regression model would be Charles’ Law which says that temperature and volume of a gas are proportional. By collecting temperatures and volumes of a gas, we can derive the proportionality constant between the two. For a multi-variable case, one example might be finding the relationship between the price of a house and its square footage and how many bedrooms it has.

It turns out we can write linear regression in terms of a graph like the one below. In this example we have two types of input data (features), \(x_1\) and \(x_2\). The function to be fit takes each of these data points, multiplies it by a weight \(w_1\) or \(w_2\) and adds them together. The \(b\) is the “bias”, which is analogous to the \(b\) in a linear equation \(y=mx+b\).

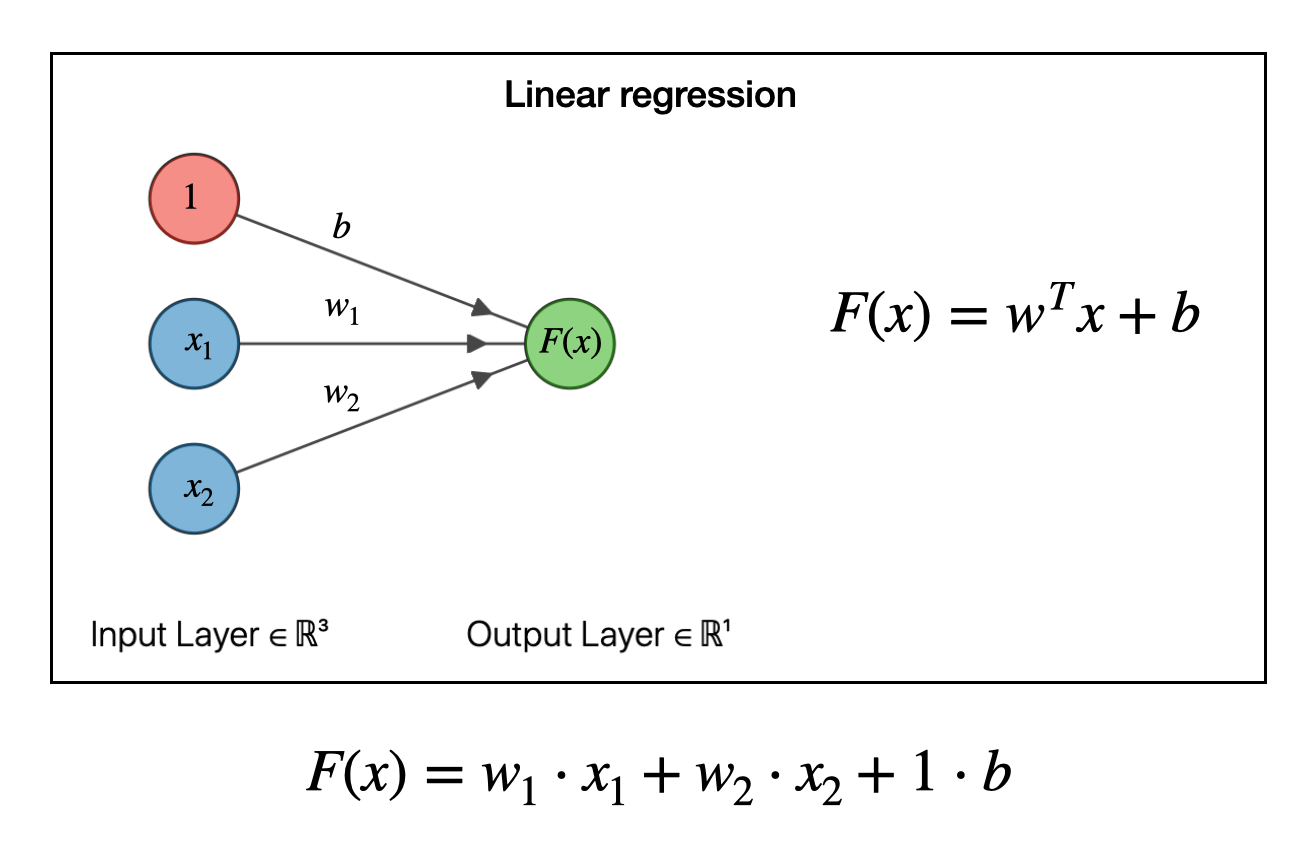
To make a model, we have to solve for the weights \(w\) and the bias \(b\). This can be done by many types of optimization algorithms (say, steepest descent or by pseudoinverse). Don’t worry about how the weights are obtained, just realize that that, one, we can obtain them and, two, once we have the weights and bias then we now have a functional relationship among our data.

So for example, if \(F(x)\) is housing price, and \(x_1\) is square footage and \(x_2\) is number of bedrooms, then we can predict the housing price given any house area and bedroom number via \(F(x) = w_1\cdot x_1 + w_2 \cdot x_2 + b\). So far so good.

Now we take things a bit further. The next step in our regression “evolution” is to pass the whole above linear regression model to a function. In the example below, we pass it to a sigmoid or logistic function \(\sigma(h)\). This is what logistic regression looks like as a graph:

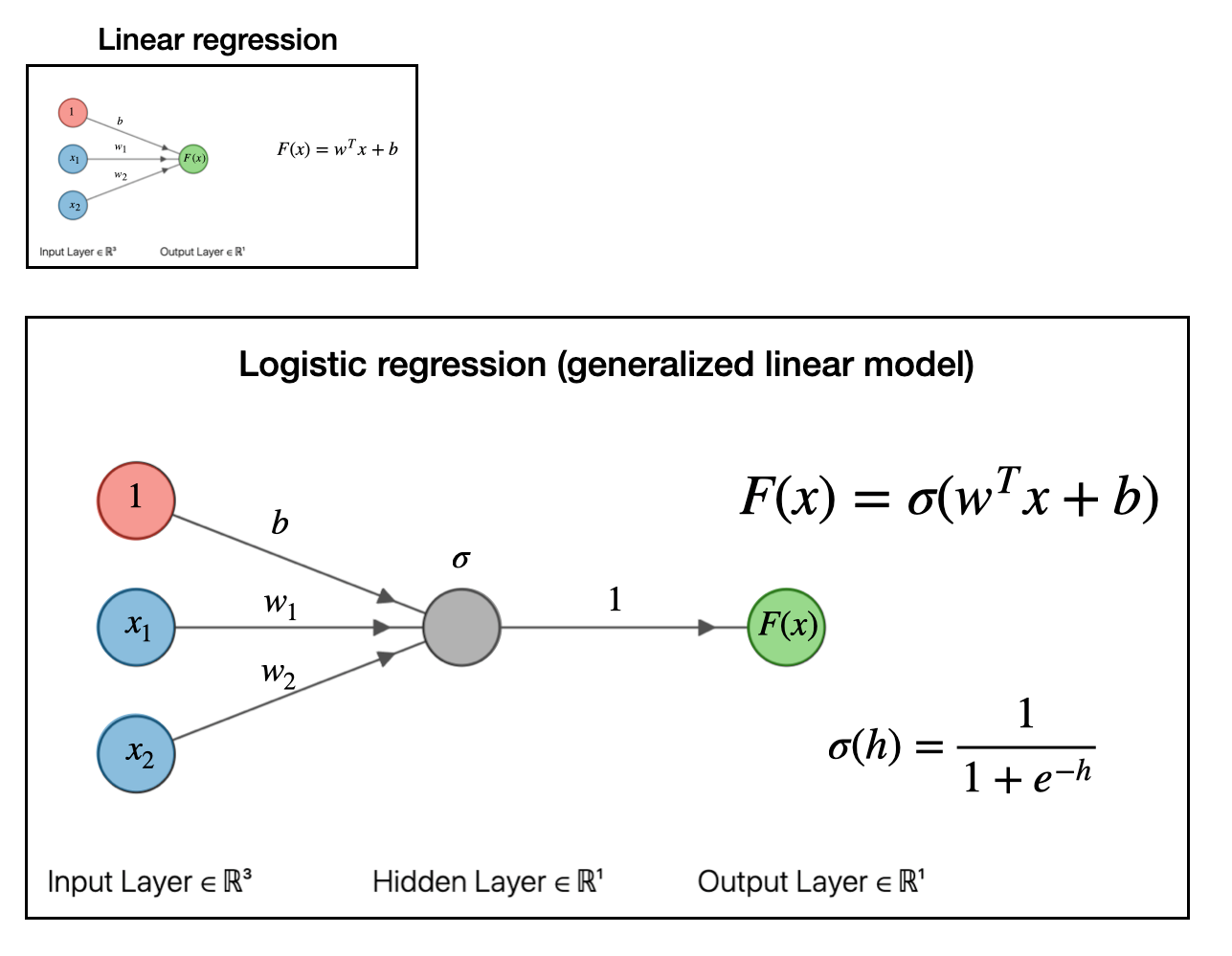
This is known as a “generalized linear model.” For our purposes, the exact function you pass the linear model into doesn’t matter so much. The important part is that we can make a generalized linear model by passing the linear model into a function. If you pass it into a sigmoid function, like we did above, you get a logistic regression model which can be useful for classification problems.

Like if I tell you the color and size of an animal, the logistic model can predict whether the animal is either a flamingo or an elephant.

So to recap, we started with a linear model, then by adding a function to the output, we got a generalized linear model. What’s the next step?

Glad you asked.

The next step with to take our linear model, pass it into a function (generalized linear model), then take that output and use it as an input for another linear model. If you do this, as depicted in the graph below, you will have obtained what is a called a shallow neural network.

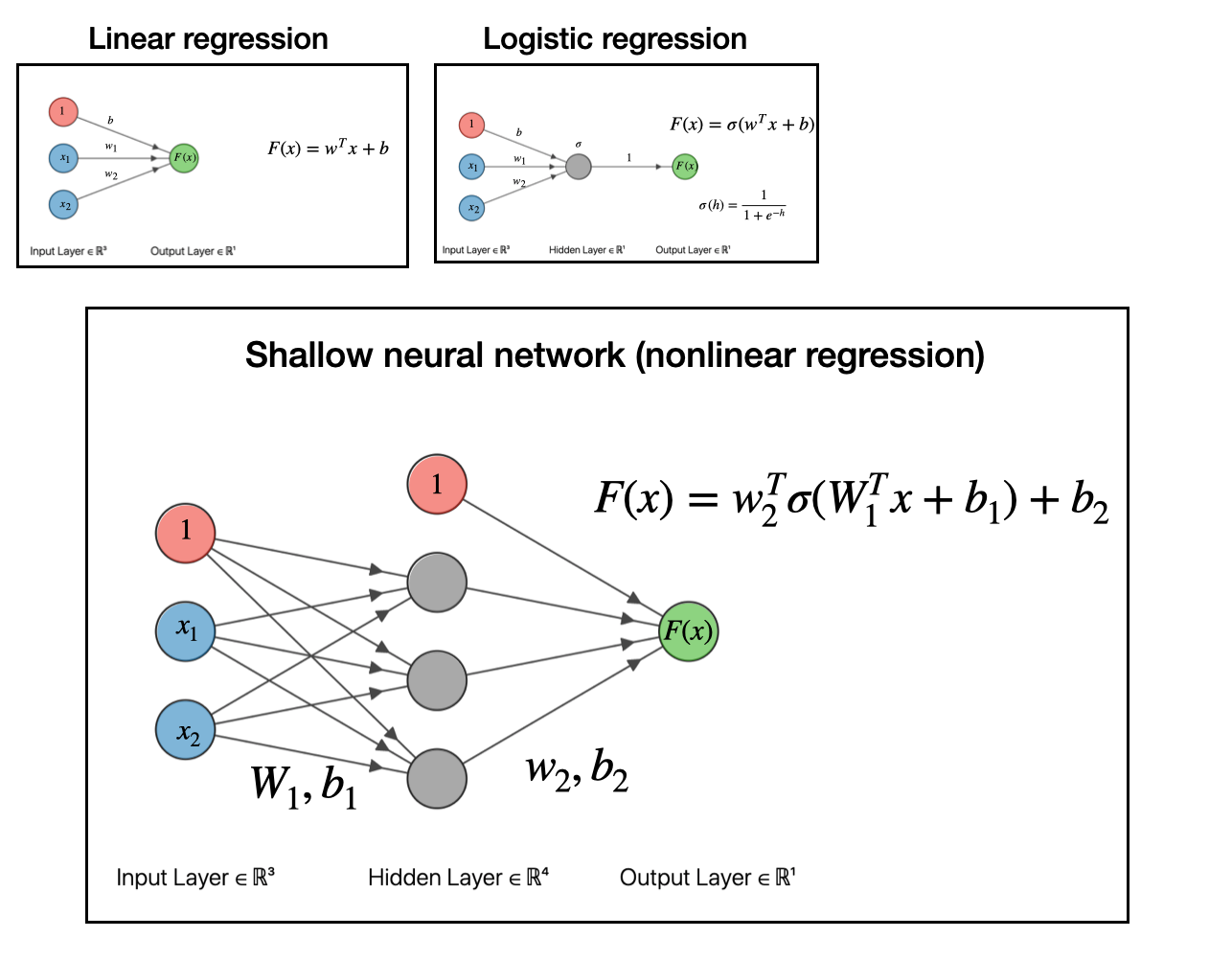
At this point, we have obtained a nonlinear regression model. That’s really all neural networks are: models for doing nonlinear regression.

At the end of the day all these models are doing the same thing, namely, finding relationships among data. Nonlinear regression allows you to find more complex relationships among the data. This doesn’t mean nonlinear regression is better, rather it is just a more flexible model. For many real-world problems, simpler linear regression is better! As long as it is suitable to handle your problem, it will be faster and easier to interpret.

So to recap, we went from linear regression, to logistic regression (a generalized linear model), to shallow neural network (nonlinear regression). The final step to get to deep neural networks is to pass the output of the shallow network into another function and make a linear model based off that output. This is depicted below:

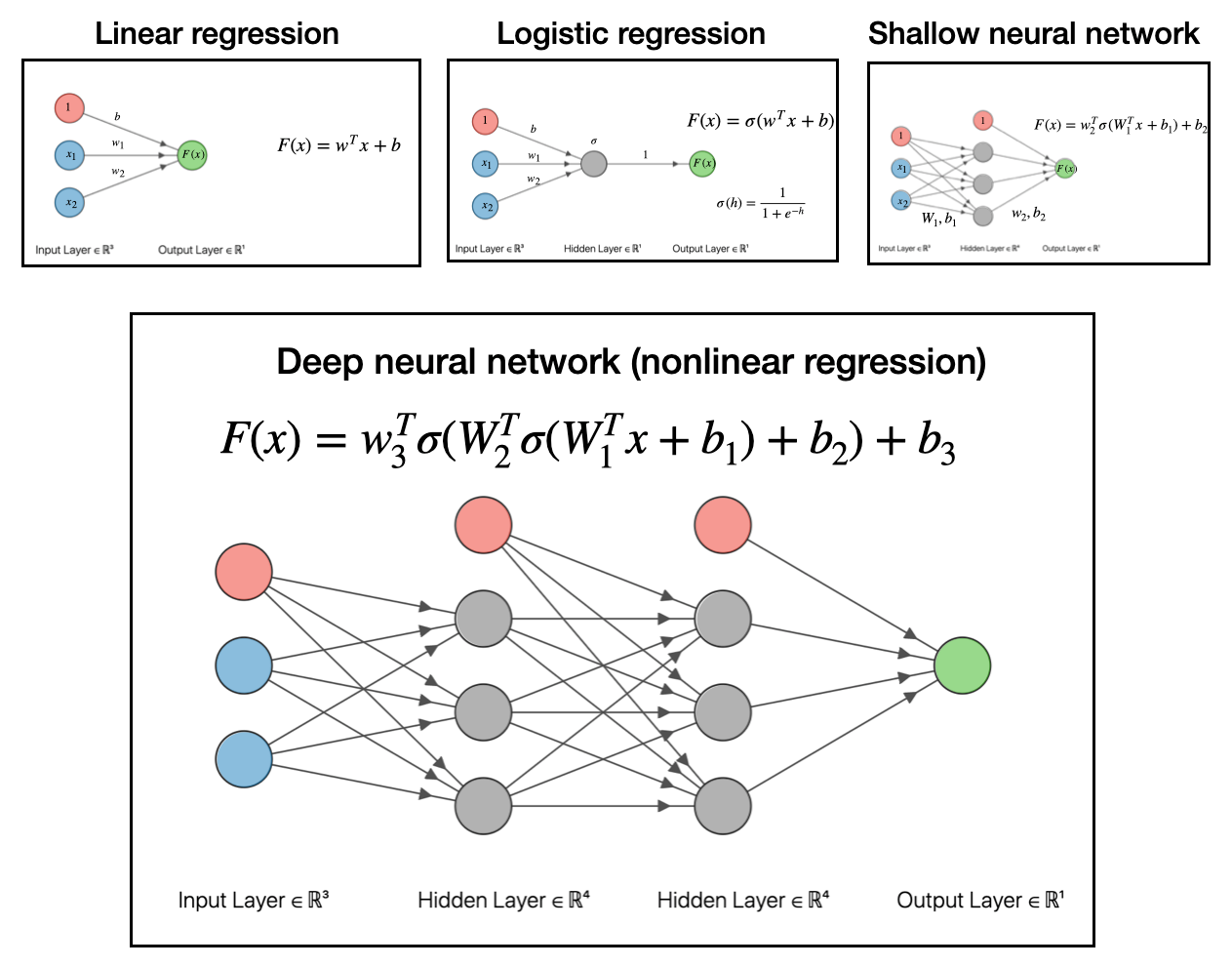
To reiterate, all these deep networks do is take data, make a linear model, transform with a function, then make another linear model with that output, transform that with a function, then make another linear model…and so on and so forth.

Data \(\to\) linear model \(\to\) function \(\to\) linear model \(\to\) function \(\to\) linear model…

It’s a series of nested functions that give you even more flexibility to handle strange nonlinear relationships among your data. And if that’s what your problem requires, that’s what it’s there for!

Obviously, modern developments of neural networks are far more complicated. I’m simplifying a lot of the details, but the general idea holds: neural networks are models to do nonlinear regression, and they are built up from linear models. They take one of the workhorses of scientific analysis, linear regression, and generalize it to handle complex, nonlinear relationships among data.

But as long as you keep in mind that it can be broken down to the pattern of passing the output of linear regression to a function, and then passing that output to another linear model, you can get pretty far.

Hope that helps!